理解AES_S-box盒生成
一开始,我以为S-box这玩意就是随便找的一个map去做substitution,但仔细研究发现原来这里面数学原理深奥去了。光S-box的生成就很有意思,核心就是求多项式的逆元和访射变化,之后有大量时间再做更深层次的分析,本次对AES中的S-box的生成做一个笔记,学习AES是为了了解它的数学设计思想,为之后理解Number theoretic transform热身。
求乘法逆元
首先,对于S-box是行从00~ff,列也是从00~ff的一个matrix,也就是有限域GF(2^8)的所有element(0~255)
1 | 00 01 02 03 04 05 06 07 08 09 0A 0B 0C 0D 0E 0F |
把每个字节看成一个多项式用来表达它的二进制形式,ai代表第i比特位的值(0或者1)
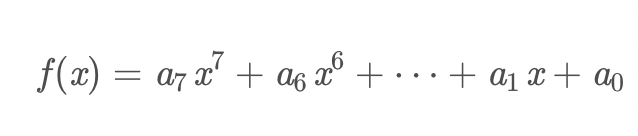
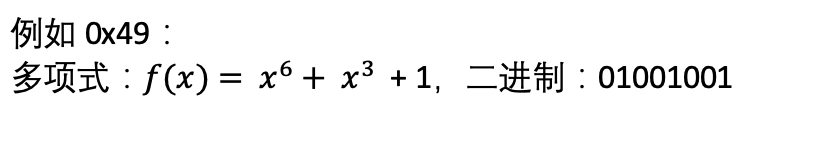
将矩阵里的所有elements都求它的乘法逆元
00的逆元就是00本身
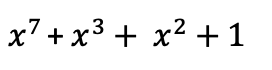
最重要的是如何计算多项式的乘法逆元,a(x)就是此时的字节,m(x)是一个固定的不可约多项式(因式只有1和它本身)
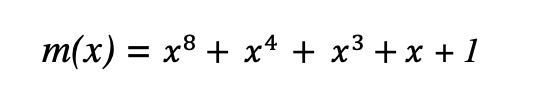
这里提一句,这个S-box的设计真的给AES带来了很强的扩展性,光m(x)其实就可以扩展使用其他的数来代替,比如下面这些,RJNDAEL选择了0x11b,也就是上述的m(x)多项式,关于这块想更了解的可以看这篇论文Generation of AES S-Boxes with various modulus and additive constant polynomials and testing their randomization
1 | 11B, 11D, 12B, 12D, 139, 13F, 14D, 15F, 163, 165, 169, 171, 177, 17B, 187, 18B, 18D, 19F, 1A3, 1A9, 1B1, 1BD, 1C3, 1CF, 1D7, 1DD, 1E7, 1F3, 1F5, 1F9. |
要求的就是b(x)
a(x) * b(x) = 1 mod m(x)
如何求多项式的乘法逆元呢?这里用到了扩展欧几里得定理
a(x) * b(x) + s(x) * m(x) = 1
这里拿02举例子,02对应的多项式为x,m(x)移到右边可以和右边的1消掉(这里的+是表示异或操作)
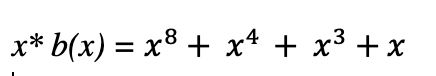
所以要求的b(x)就是
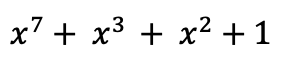
S-box还可以用xtime的方法更高效求逆元,具体可以参考b站这个小姐姐讲的现代密码学|AES数学基础|GF(2^8)有限域上的运算问题
仿射变化
求出了02的逆元10001101后,利用下面的矩阵运算做仿射,bi就是10001101的各个比特位的值

其实就是下面的公式(需要注意的是用到了LSB,表示低位在前,所以63的二进制是从下往上依次为01100011)
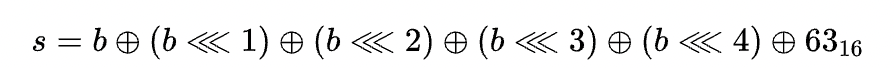
经过这轮变化后,计算出来02对应S-box中的值为7B,对照S-box表也是这个数,验证成功

关于代码实现还有仿射变化的深入理解,之后有空再总结,涉及的数学原理就太深了,光目前为止,就感受到了这些数学方法带来的扩展性和目的
By the way, “If you’re typing the letters A-E-S into your code, you’re doing it wrong.” - Thomas Pacek

