初识测信道攻击(Side Channel Attack)
初识测信道攻击(Side Channel Attack )
目前测信道攻击的几个攻击面:热量,声音,时钟,电磁辐射,能耗。为什么从这些面去攻击呢?因为这些面都是非常轻易能测量的!也是开发者很难做防守的点。我将从能耗攻击入手测信道,定期分享一些心得。
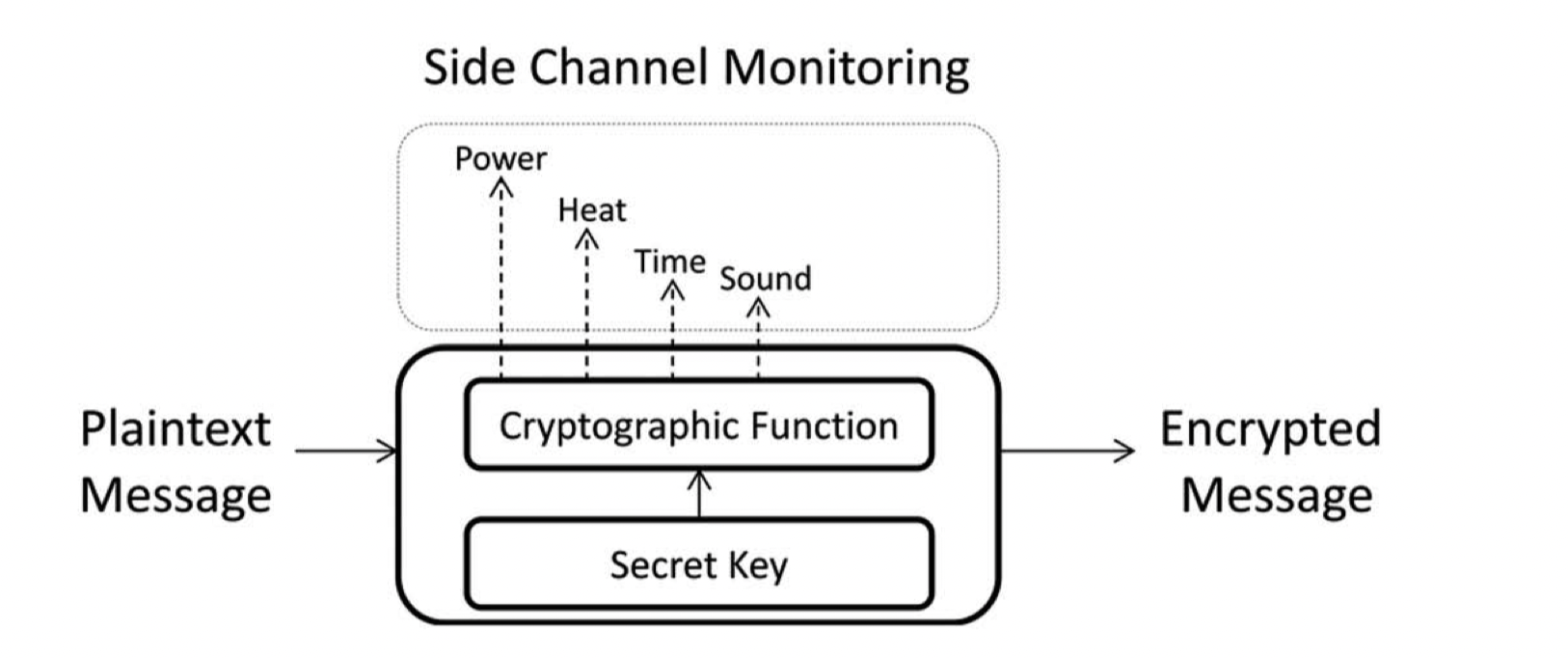
能耗攻击AES加密算法,简单来说就是通过监控设备在加密过程中的能耗来推测AES加密的密钥。而其中的推测方式主要有两种,一种是DPA(利用平均数的差分),另一种是CPA(利用统计学推测能耗与数值间的相关性)。其实它两本质上是一样的道理,只不过是在处理能耗数据上采取了不同的策略,殊途同归。在了解主要的两种能耗攻击(DPA和CPA)的具体过程之前,这里简单介绍一下AES-128加密算法
AES-128加密算法
Step1: AddRound key
明文P和密钥K,我们可以将其分别看成两个4x4的矩阵,每个Value都是一个字节。让两个矩阵进行+操作。
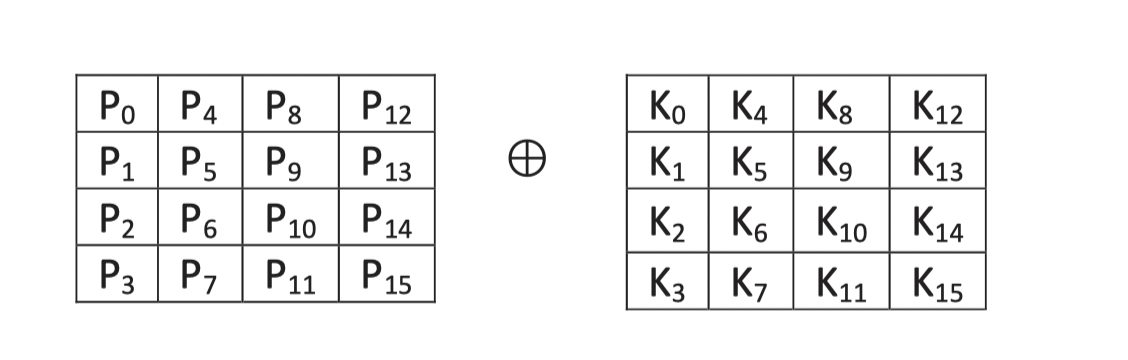
操作如(3),简写成(4)
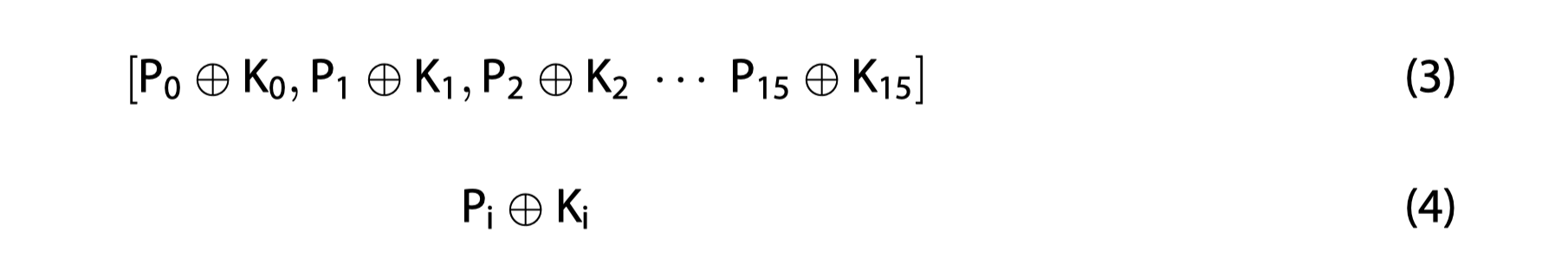
Step2: SubRound
在AddRound后,得到一个4x4的新矩阵,这还不够,AES还想让这些数据做更大的混合,加大破解的难度,于是乎通过一个叫S-box的东西把Round后的每一个数值进行固定的替代。例如Round后的一个字节是0x12,那么就找到第0x1行,第0x2列的数值,这个表中是c9,那么就是把0x12换成c9。这样换下来后,数据的破解难度会加大。

SubRound过程这样表示
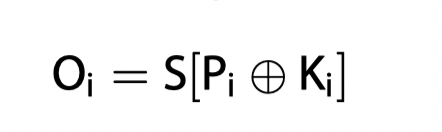
下面一个例子是在AddRound后的矩阵做SubRound后的结果,可以看到数值都通过S-box准确映射成一个新的矩阵

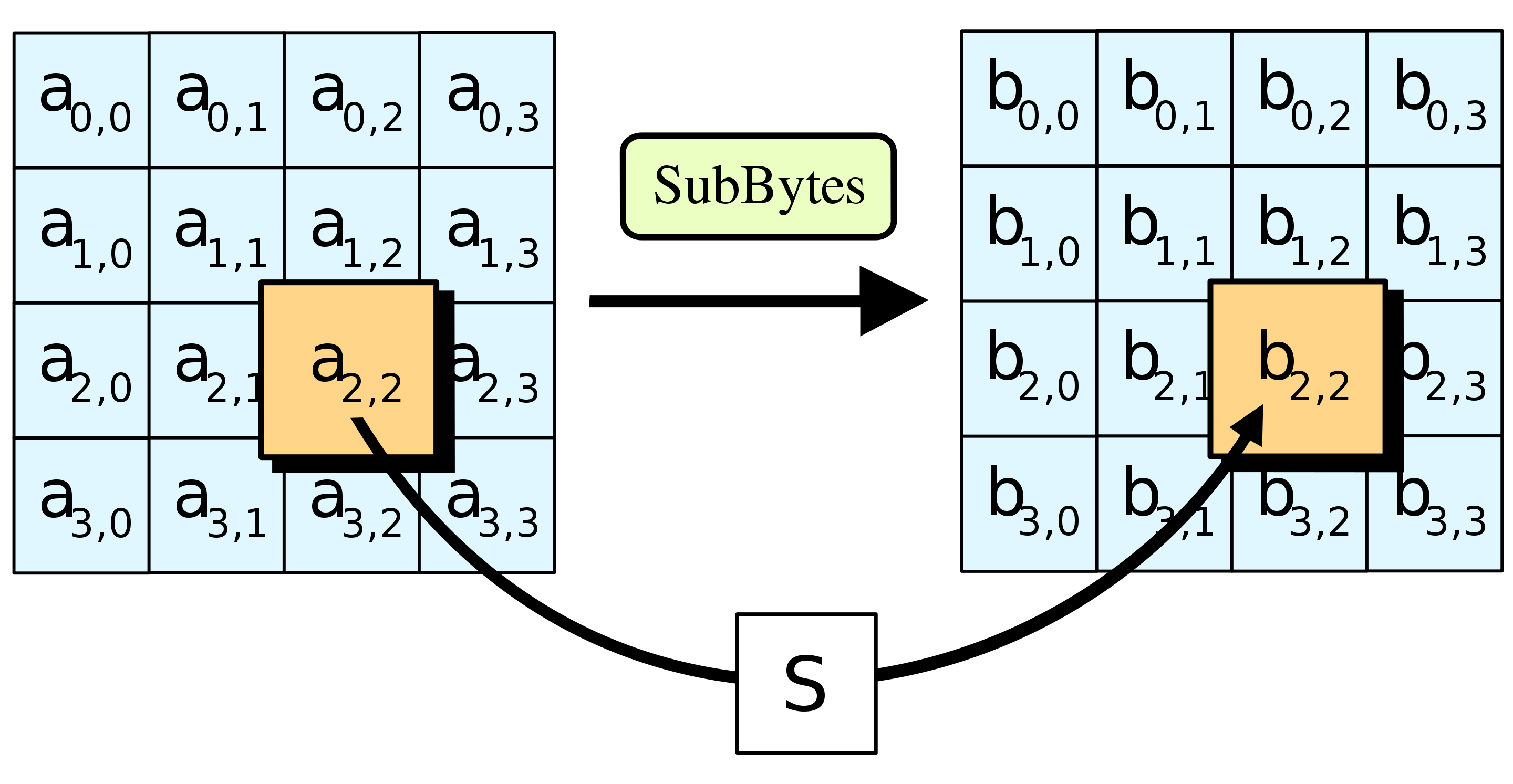
Step3: ShiftRows
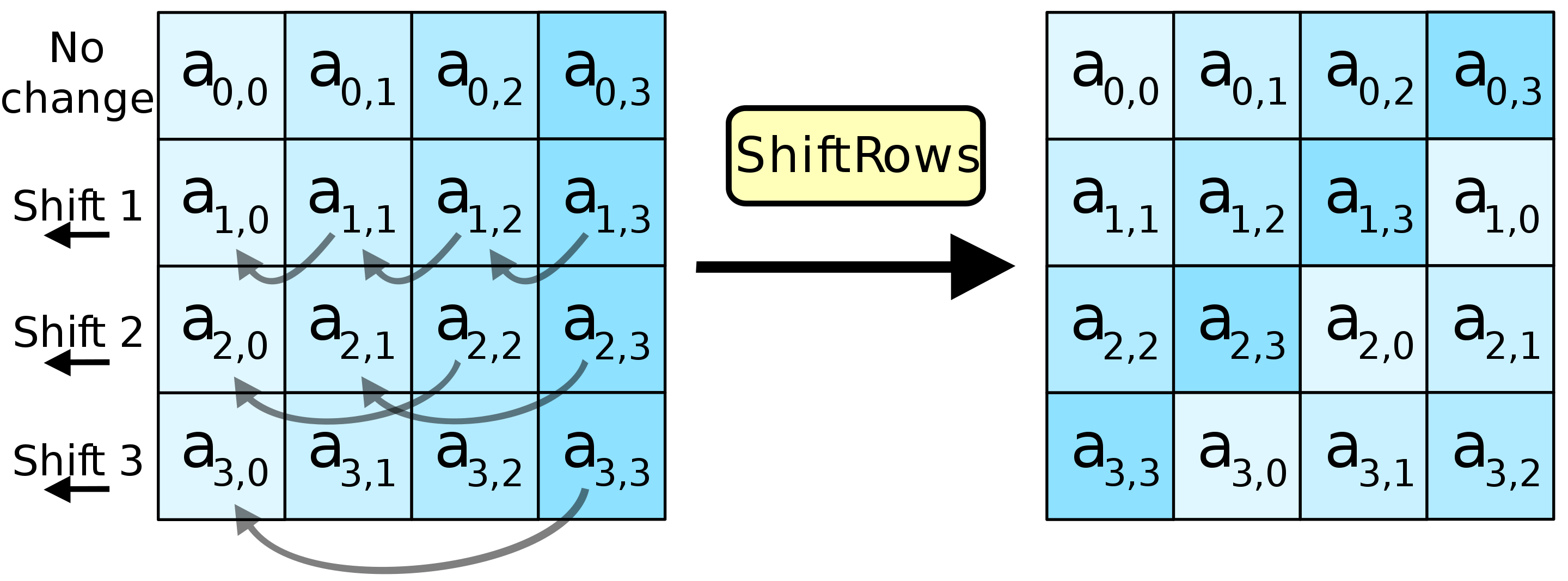
把上一步得到的矩阵的行进行左移,第i行左移动i位(从0行开始数),第0行不移动,第一行一动一位,第二行移动两位以此类推。。。然后得到一个新的矩阵
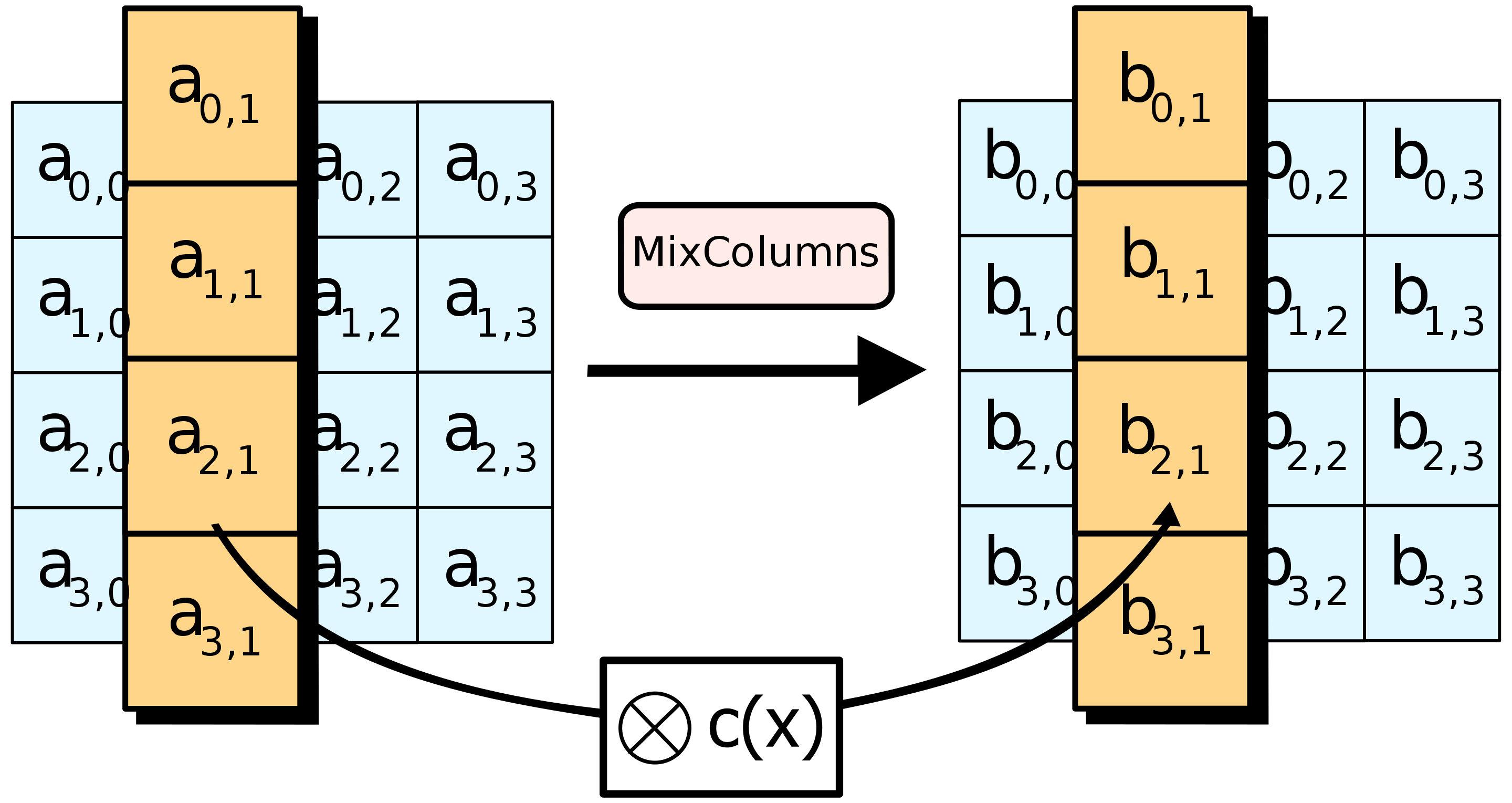
Step4: MixColums
将上一步得到的矩阵和一个固定的矩阵进行乘操作又得到一个新的矩阵
根据维基百科,这个矩阵貌似是固定的,就是下面这个
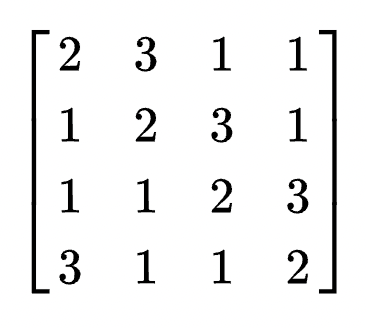
可以发现就是三种情况,乘1,2,3。然而需要注意的是这个乘法很特殊不像十进制那样。
第一种情况:1*a = a
第二种情况:2*a,如果a的首位是0,那么a左移2位,如果a的首位是1,则( (a<<1) & ( (1<<8) - 1) ) ^ (0x1b)
第三种情况:3*a,则(2 * a) ^ a
Step5: AddRound key
再来一遍AddRound key,但此时的key不再是原来的了,需要通过原来的密钥进行计算。把原来的密钥按列看成4个字节,每个字节进行左环移,然后又对这4个字节进行S-box变换,变换后,最左面的字节与RCj相加,AES128加密要把以上步骤进行10轮,RCj在每一轮的计算中都不一样
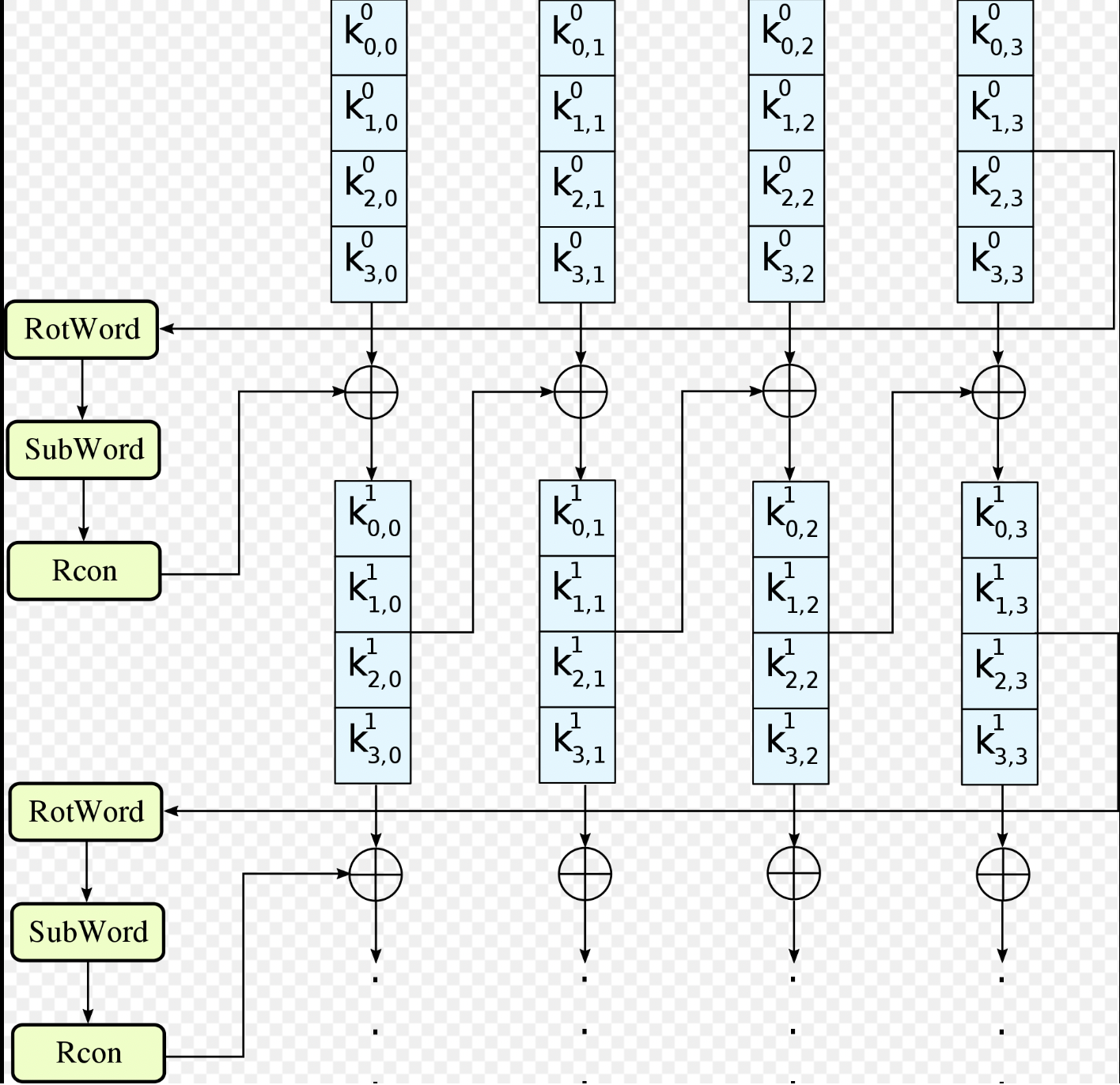
RCj在每一轮中对应的数值如下:

Step6: Optimization of the cipher
把上述过程重复10次,最后得到的就是16字节的密文了
DPA(Differential Power Analysis)
通过分析设备在执行密码操作时消耗的电力来获取信息。攻击者会收集大量的电力消耗数据,然后分析这些数据来寻找模式和差异。这些模式或差异可以帮助攻击者猜测密钥的部分或全部。
步骤:
数据收集:用电脑通过串口对板子发送指令信号去执行AddRound Key和SubBytes操作。AddRound和SubBytes为每个单独的明文运行10次,以使示波器能够得到一个平均的结果(从而帮助减轻背景噪音和干扰)。
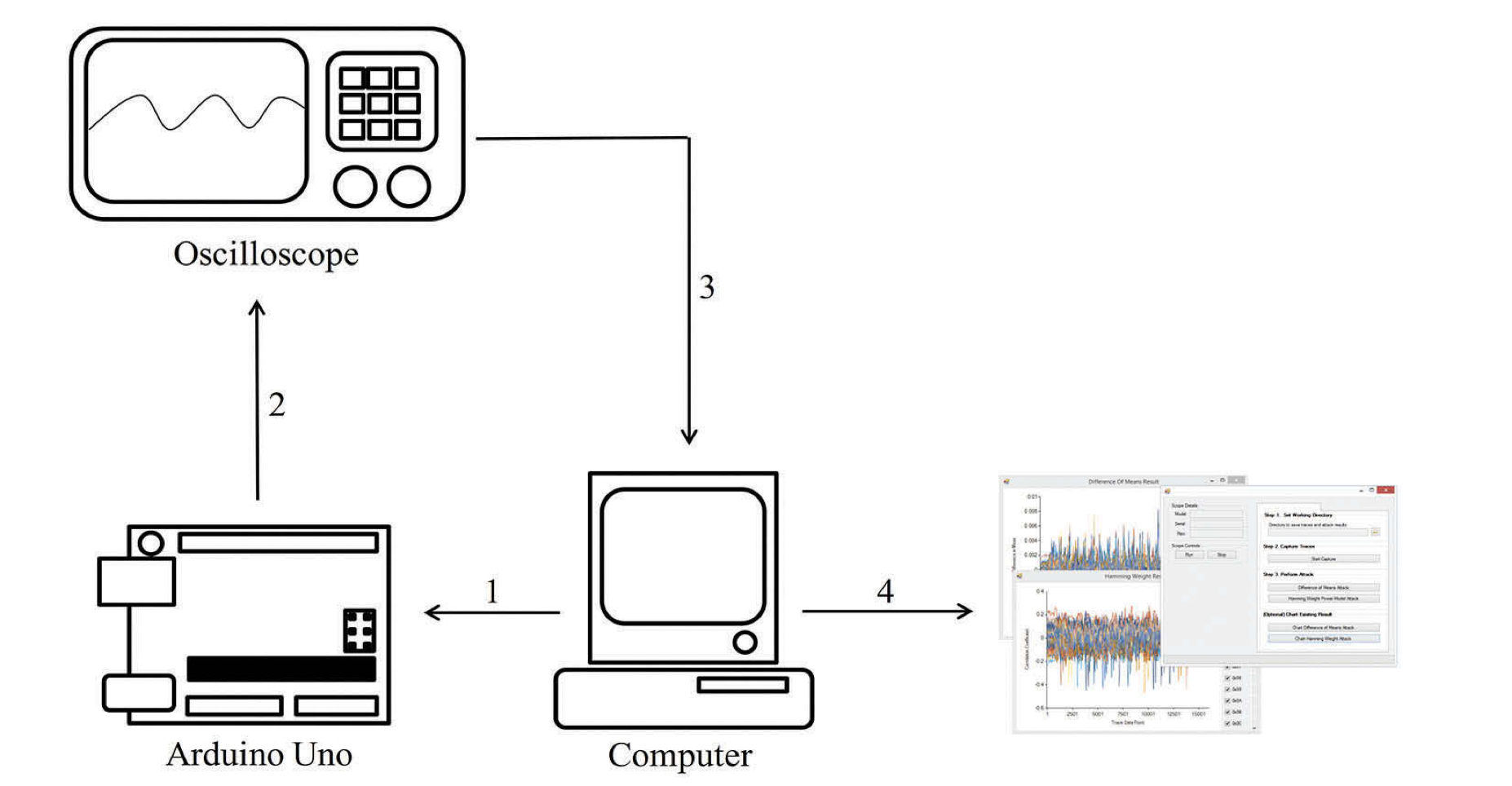
在CMOS电路中,对位为1的数据进行操作通常需要更多的电荷移动,因此消耗更多的能量。观察LSB(the least significant bit,最低有效位)。如果该假设成立,我们可以利用这个事实在密码操作期间推导出密钥。功耗其实变化是非常小的,几乎没法用肉眼观察,因此,在DPA中,必须收集大量的迹线,根据LSB的值将这些功耗迹线数据分成两个子集:一个子集包含LSB为0的迹线,另一个子集包含LSB为1的迹线。
假设有一个只有两位的简单加密系统,采用XOR操作作为加密操作,我们有四种可能的密钥(00,01,10,11)。(假设功耗只和明文中的1的数量有关,实际情况会更复杂。)
1 | 明文 密文 功耗 |
分组:我们可以预测明文和每个假设的密钥进行XOR操作后的中间值。对于每个假设的密钥,我们将功耗样本按照预测的中间值的最低有效位(LSB)进行分组。例如,对于假设的密钥01:
1 | 明文 XOR 密钥 = 中间值 |
这样我们就得到了两组功耗样本:
1 | 0组:[2.0, 1.0] |
计算差分:我们计算每组的平均功耗,然后计算两者之间的差值。在这个例子中,0组的平均功耗是1.5,1组的平均功耗也是1.5,差值为0,说明01不太可能是密钥,之后代入其他的比如00,11,10,谁的差分最大谁才是最可能的密钥。
密钥选择:我们将重复这个过程,对每一个可能的密钥都计算出一个功耗差值。最后,我们将选择那个使得功耗差值最大的密钥作为可能的正确密钥。在这个极度简化的示例中,所有的密钥都会得到相同的差值,所以我们不能确定正确的密钥。但在实际情况下,正确的密钥通常会导致较大的功耗差值。
密钥猜测选择方法:
以上是一个数据量非常小的例子,枚举所有数值即可,而实际的AES-128,密钥是128位(16个字节),枚举所有可能去一个个套是不可能的。在进行密钥猜测时,可以采取以下几种方法:
字典攻击:创建一个包含可能的密钥的字典,并将每个密钥尝试应用于攻击目标。这需要预先生成和存储大量可能的密钥,并进行遍历比较。然而,由于密钥空间非常大,这种方法很可能会遭遇到时间和空间上的限制。
蒙特卡罗方法:使用随机生成的密钥进行攻击,并观察功耗模式。重复这个过程多次,根据每个密钥产生的功耗模式的统计信息来推断出最有可能的密钥。
高级优化算法:使用各种优化算法(如遗传算法、模拟退火算法等)对密钥空间进行搜索。这些算法可以在密钥空间中进行智能搜索,以找到可能的密钥。
辅助信息攻击:尝试收集更多关于目标设备的辅助信息,例如设备在处理不同输入时的功耗变化模式,或者算法执行中的其他侧信道信息。这些额外的信息可以用于提高密钥猜测的准确性。
CPA(Correlation Power Analysis)
这是一种更为复杂的攻击,利用了电力消耗与密钥操作之间的统计相关性。具体来说,攻击者会生成一系列密钥假设,并对每个假设进行电力消耗模型的计算,然后将这些结果与实际的电力消耗数据进行相关性比较。假设与实际数据相关性最高的密钥最有可能是正确的密钥。
步骤:
收集侧信道数据(这些数据可以是设备的功耗消耗曲线、电磁波辐射强度或其他与设备操作相关的信号。因为DPA已经举了能耗的例子就不在此赘述了。
建立模型:接下来,需要建立一个统计模型来描述侧信道数据与秘密密钥之间的关系。通常使用相关性分析来构建这个模型。举一个与DPA类似但略有不同的点。
相关性:在DPA中,我们是只考虑了LSB,通过LSB这一个角度去分析数据。而在CPA中,我们可以选择更多可能的相关性。在功耗分析攻击中使用Hamming Weight Power Model的假设是输出的0或1位的数量与设备的功耗消耗存在相关性。比如二进制1001110,在DPA中,就只考虑最低位是0,分析的数据的相关性其实比较弱。而CPA中,我们可以选择以评判这个二进制中1的数量,比如二进制11111111,有8个1,二进制11001100只有4个1。1多的数消耗的能耗要多于1少的。
1 | value P |
统计分析:下图给出了一个加密设备可能产生的输出示例以及测量每个输出时的功耗消耗。输出为0000 0111的汉明重量为3,而0000 1111的汉明重量为4,依此类推。

假设我们生成了一个完全准确的汉明重量功耗模型,那么如图所示,将会找到强正相关性(即随着功耗消耗的增加,二进制输出中的1的数量也会增加)。
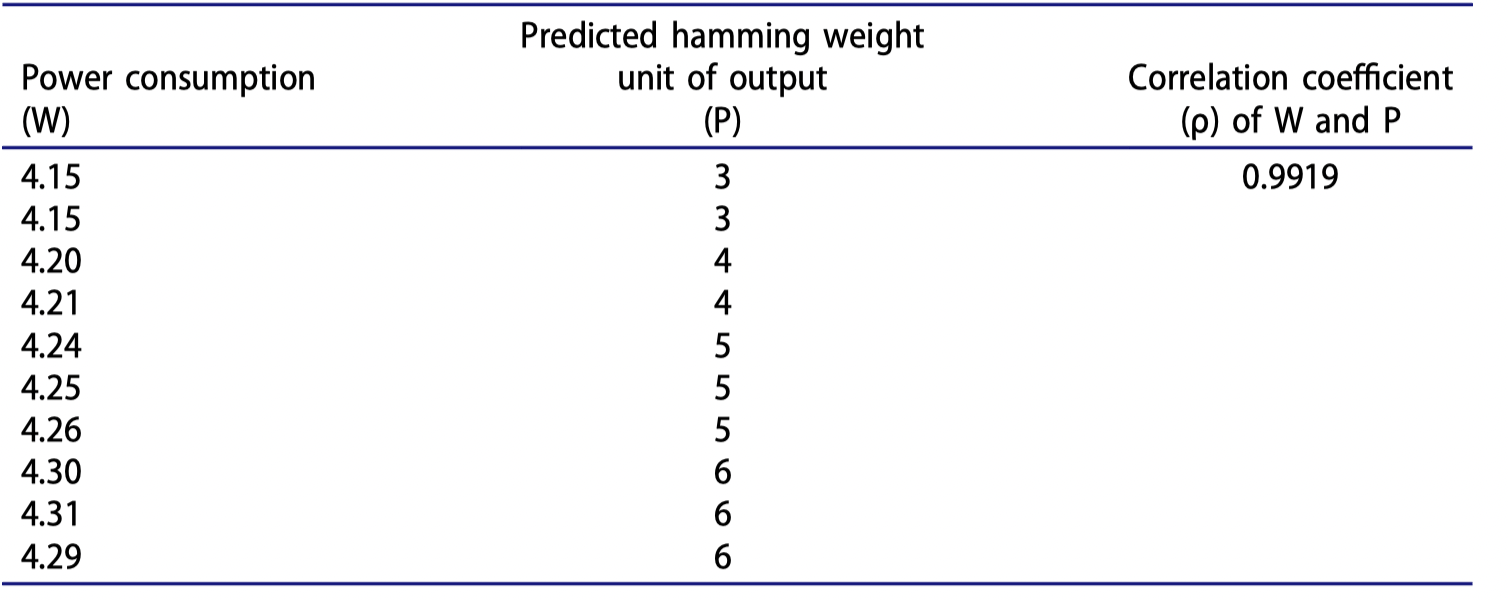
密钥推断:根据统计分析的结果,可以推断出猜测的密钥位的值。在我们的例子中,如果发现某个时间点上的功耗值与猜测密钥的第一个字节的值呈现高度相关性,那么我们可以得出结论,猜测的密钥位的值可能是正确的。
验证和重复:对于成功推断的密钥位,我们可以使用其他的加密操作或数据样本进行验证。如果验证成功,则可以进一步推断其他未知的密钥位。如果验证失败,则需要重新进行攻击过程,并尝试不同的猜测和分析方法。
总结
破解密钥就像仿制一个特定的杯子,数据就像水,杯子可以让水变成多种形状就像密钥可以改变数据到面目全非,而破解密钥的过程就是不断尝试利用各种方法雕刻杯子直到能和特定杯子一样能使数据的形状一致。

